Animals live in dynamic environments that rapidly evolve into new, unfamiliar arenas of survival — but biology does not rebuild the brain for every challenge. Useful computations are conserved across eons of evolutionary design. A universal neural computer, the brain assembles robust, flexible solutions to problems it has never seen before with a reliability state of the art machine learning (ML) systems lack.
This project studies the modular hypothesis for universal neural computation. Modularity refers to the extent a system can be divided into autonomous and reusable components, termed modules. Each module specializes in solving a sub-problem and each modules’ solution is assembled to solve the full problem. Numerous studies have shown that the neurophysiology of vertebrate higher cortex is highly modular. Modular organization, and the coordination strategy among modules, are thought to endow the cortex with a capacity for adaptive task-specialized computation. Theoretical neuroscience seeks answers to several questions about the modular organization of higher cortical areas: a) What are the computations performed by cortical modules? b) How is sensory information distributed to and shared across modules? and c) How are the modules’ individual computations recombined to flexibly solve a variety of tasks, old and new?
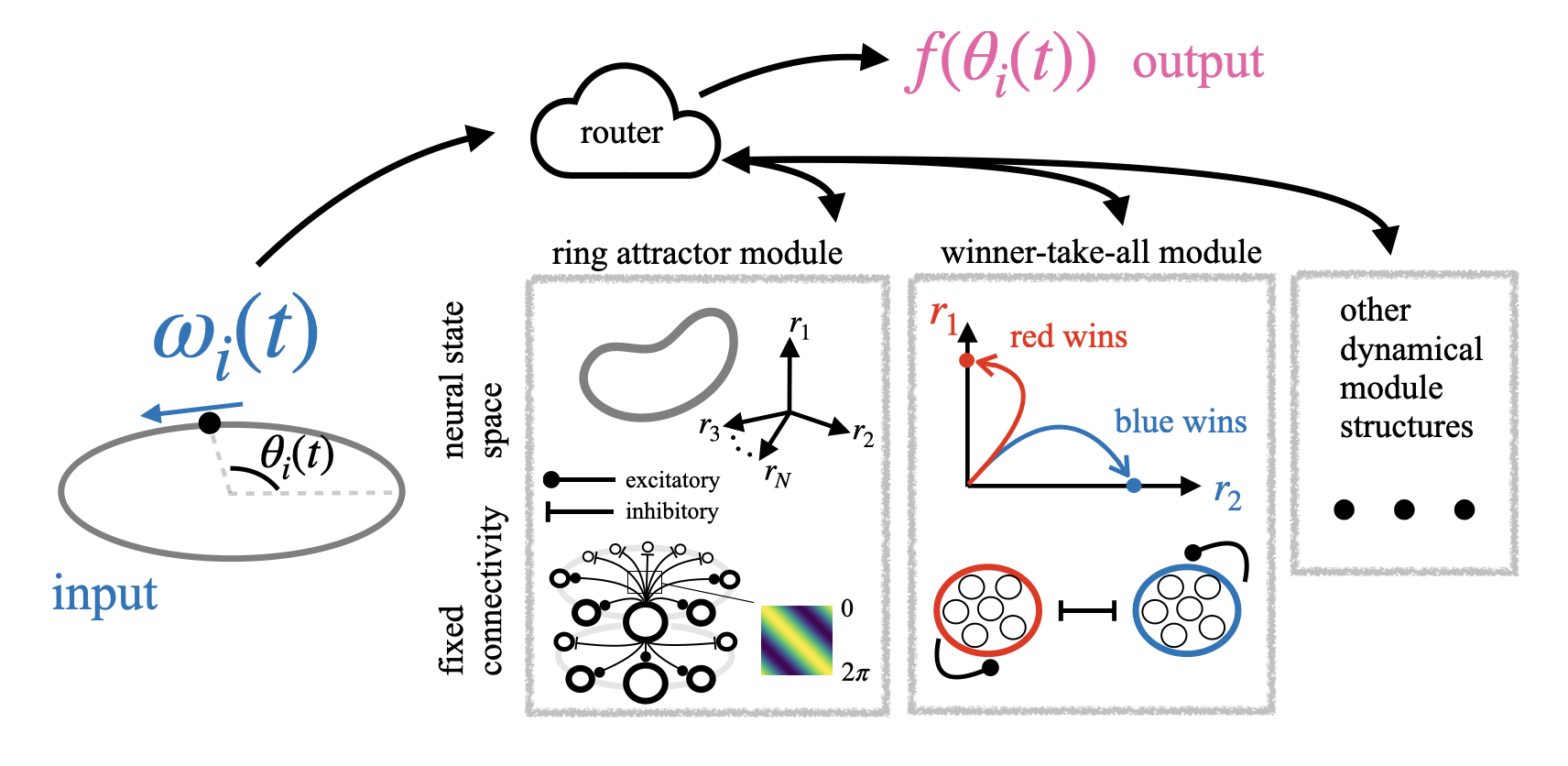
Tying these questions together is the information routing problem. Given an input and a task, a modular neural network must route information from input to modules, compute sub-solutions with each module, then synthesize these sub-solutions to complete the task. My research targets these questions and presents a solution whereby modules implement canonical and well-understood computations, together with a generic compositional strategy to route information from input to modules to output. This approach holds promise for transforming the design of interpretable ML architectures capable of robust, flexible, and universal brain-like computation.
The attractor network is a widely observed computational primitive in biological brains. Using attractor subnetworks as modules, my goal is to construct a canonical basis for universal neural computation with attractor dynamics as primitives. Neurons in each module are fixed with prescribed connectivity endowing their activity with attractor dynamics. These dynamics have been shown to explain how the brain maintains persistent activity patterns for working memory, tolerates noise perturbations, and integrates sensory inputs. Many real-world tasks can be decomposed into a set of computations performed by attractor networks. A network imbued with a rich set of such computations, together with a compositional routing strategy, could achieve general-purpose neural computation.
A pre-print is forthcoming.